Tangentialebene - DDDEasy
Wortinformationen
Artikel: die
Wort: Tangentialebene
Typ: Substantiv
Silbentrennung: Tan•gen•ti•al•ebe•ne
Duden geprüft:
PowerIndex: 5
Häufigkeit: 2 von 10
Wörter mit Endung -tangentialebene: 1
Wörter mit Endung -tangentialebene aber mit einem anderen Artikel die : 0
Das Wort wird häufig verwendet im Bereich Mathematik
89% unserer Spielapp-Nutzer haben den Artikel korrekt erraten.
Tangentialebene Wiki
Author: Hellingspaul
Lizenz: Creative Commons Attribution-Share Alike 3.0
Bild:Wikimedia
Wortbeschreibung : Wikipedia
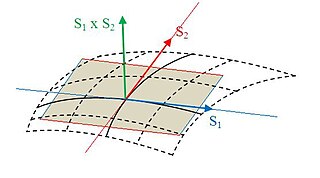
Die Tangentialebene in einem Punkt
an eine Fläche
im dreidimensionalen Raum ist diejenige Ebene, die die Fläche in der Umgebung des Punktes
am besten annähert (berührt). Sie ist damit die zweidimensionale Entsprechung zur Tangente einer Kurve. Wie im Fall der Kurve existiert eine Tangentialebene nur, wenn die Fläche hinreichend „glatt“ ist. Dies gilt zum Beispiel für die Graphen von differenzierbaren Funktionen von zwei Variablen. Eine Fläche, die einen Knick oder eine Spitze hat – zum Beispiel ein Kegel – besitzt in diesen Punkten keine Tangentialebene.